06838083 陳書勤 HW4

空間濾波(Spatial Filtering)

空間域v.s頻率域

影像在傳輸過程中，由於受到通道、劣質取樣系統以及其他的幹擾影響，導致影像變得粗糙、不清晰而產生雜訊，雜訊產生的原因決定了雜訊與影像訊號的關係。

圖像的處理中，圖像的頻率域是圖像像元的灰度值隨位置變化的空間頻率，以頻譜表示資訊分佈特徵，傅立葉轉換能把遙感圖像從空間域變換到只包含不同頻率資訊的頻率域，原圖像上的灰度突變部位、圖像結構複雜的區域、圖像細節及幹擾雜訊等資訊集中在高頻區，而原圖像上灰度變化平緩部位的資訊集中在低頻區。只是說要將圖像變換到另一種域中，然後有利於進行處理和計算比如說：圖像經過一定的變換（Fourier變換，離散yuxua DCT 變換），圖像的頻譜函數統計特性：圖像的大部分能量集中在低，中頻，高頻部分的分量很弱，僅僅體現了圖像的某些細節。降低影像的雜訊成分即減少雜訊的方法可分為兩種：一種是在空間域做處理，另一種則是在頻率域上做處理。

頻率域(frequency domain)又稱頻域。是描述信號在頻率方面特性時用到的一種坐標系。對於一個信號來說，它有許多方面的特性。如信號強度隨時間的變化規律（時域特性），信號是由哪些單一頻率的信號合成的（頻域特性），頻率域就是平常我們用的是時域，是和時間有關的，這裏只和頻率有關，是時間域的倒數。時域中，X軸是時間，頻域中是頻率，頻域分析就是分析它的頻率特性！

空間域(space domain)又稱圖像空間(image space)。由圖像像元組成的空間。在圖像空間中以長度(距離)為引數直接對像元值進行處理稱為空間域處理。

圖像的空間域是指圖像平面所在的二維平面，對於空間域的影像處理主要是對像元灰度值的改變，其位置不變。

空間頻率域(spatial frequency domain)是以空間頻率(即波數)為引數描述圖像的特徵，可以將一張圖像的像位值在空間上的變化分解為具有不同振幅、空間頻率和相位的簡振函數的線性疊加,圖像中各種空間頻率成分的組成和分佈稱為空間頻譜。這種對圖像的空間頻率特徵進行分解、處理和分析稱為空間頻率域處理或波數域處理。

空間頻率，就是在每單位長度上，出現幾個同樣的幾何結構。

如果同樣的幾何結構重複的距離為λ，那空間頻率就是λ的倒數。

這個概念與力學中的波動類似，λ可以視為週期T，f就是頻率ν。k = 2 π ν = 2 π λ {\displaystyle k=2\pi \nu ={\frac {2\pi }{\lambda }}}

下圖中(b)、(c)和(d)的空間頻率分別是(a)的2倍、4倍和8倍。

直接針對空間域上的圖元色彩值進行處理，處理結果也是直接取代原先空間域上的圖元色彩值。

並不會直接針對空間域的圖元色彩值處理，會先將其換成頻率域上的係數後再進行處理，之後再轉換回來。

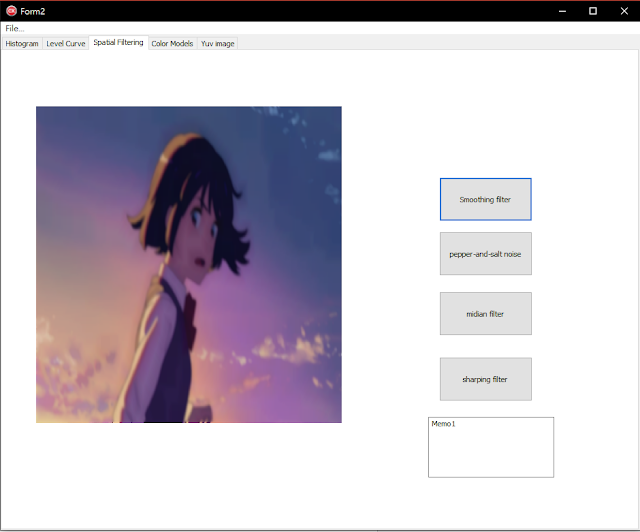
空間濾波的基本原理

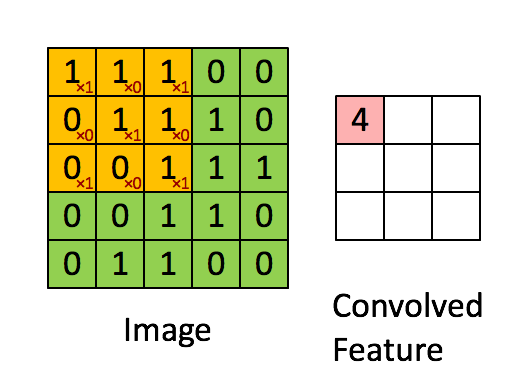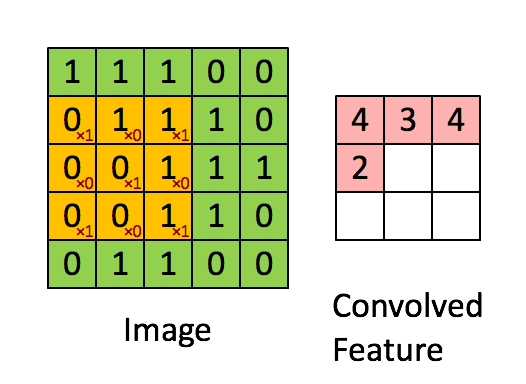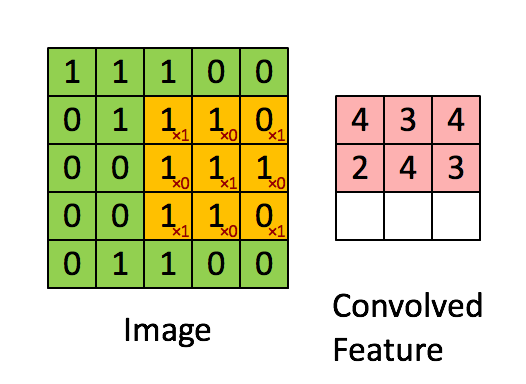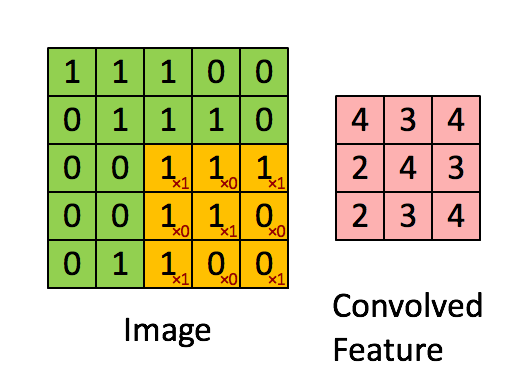
空間濾波是現在許多熱門美顏自拍、修圖的手機軟體的濾鏡處理技術應用，本單元所介紹的平滑 (Smoothing)、銳化 (Sharping)及中值等濾波器，都是屬於空間濾波的影像處理。其原理是透過一個基數的方陣(如3*3、5*5)的遮罩，將所要修改的圖元點放至中間位置，即會得到此點的色彩值與他鄰近圖元的色彩值，再根據這些值去做修改。

以下就讓我們來介紹常見的濾波器

平滑濾波器：用於模糊化和去除雜訊。

低通濾波器 (Low pass filter) 、中值濾波器 (Median filter)

銳化濾波器：強化物體的邊緣位置。

高通濾波器 (High pass filter)

平滑濾波器(Smoothing filter)主要用在影像的模糊化和減少雜訊的處理。平滑線性空間濾波器的輸出是濾波器遮罩的鄰域所含圖元的平均，這些濾波器有時候被稱為平均濾波器(averaging filters)或稱為低通濾波器(lowpass filters)。以濾波器遮罩所定義之鄰域中灰階的平均值取代影像中的每一個圖元，這樣的程式產生在灰階上「銳利」變化降低的影像，因為隨機雜訊通常在灰階上含有銳利的變化，所以平滑濾波器最明顯應用是在減少雜訊。

注意！在實作時，分母為遮罩中所有係數的總和。因此可事先計算並儲存為常數。不必於每個圖元中重新計算。

 平滑濾波器

  

             原始圖片                                模糊化

近來人工智慧蓬勃發展，除了將影像模糊化，亦可透過機器學習，處理影像的模糊或失焦等問題，甚至將不想出現在照片中的物體透過遮罩將其移除，可說是一大突破性的應用。

中值濾波器(median filter)相當受歡迎，因為對於某種隨機雜訊，它們提供了絕佳的雜訊降低效能，常可用來消除脈衝雜訊。中值濾波器是將圖元的值用該圖元(圖元的原始值包含在中值的計算內)近鄰灰階的中間值來取代，比起同樣大小的線性平滑濾波器有顯著較小的模糊化。

中值濾波器在脈衝雜訊出現時特別有用，影像中的脈衝雜訊是以白點或黑點的形式出現，看起來就像是影像中撒上黑胡椒與白鹽一般，所以又稱為胡椒鹽雜訊(Pepper-and-salt Noise)。

原始圖片	加入雜點	去除雜點

銳化濾波器(sharping filter)的目的是強化影像細節，並凸顯其色彩強度的變化。銳化處理的主要目的是突出圖像中的細節或者增強被模糊了的細節，銳化處理可以用空間微分的處理來增強圖像邊緣和其他突變並削弱灰度變化緩慢區域。

圖像銳化常採用的有微分運算和頻域高通濾波法，這裡主要針對微分運演算法。能夠進行銳化處理的圖像必須要求有較高的信噪比，否則圖像銳化後圖像信噪比更低，因為銳化會使噪聲收到比信號還強的增強，必須謹慎處理。

一般先去除或減輕幹擾噪聲後，才能進行銳化處理。

銳化空間濾波器

原始圖片	銳利化

微分運演算法主要有梯度法和拉普拉斯運算元。
1.基於一階微分的圖像增強——梯度法
對於圖像f(x,y)，它的梯度是一個向量，表示為

這個向量的模值有下式給出：

在實際操作中，常用絕對值代替平方與平方根運算近似梯度的模值：

這個公式計算起來較為簡單並且保持有灰度的相對變化，但各向同性特性通常就不存在了。

對數字圖像而言，用微分運算不方便，一般用查分運算來近似，常用的差分有：

2.基於二階微分的圖像增強——拉普拉斯運算元

對一個連續函數f(x,y),它在位置(x,y)的拉普拉斯值定義如下：

在數字圖像中，計算函數的拉普拉斯值也可借助各種範本實現。常用的兩種如下:

3.圖像銳化演算法主要包括三方面內容：

 3.1選取合適的梯度運算元（拉普拉斯、羅伯茨、索貝爾）

 3.2根據所選用的梯度運算元對圖像各點的灰度值進行計算，得出各圖元點的梯度值
 3.3根據各圖元點的梯度值選取合適的處理方法（使用梯度替換原灰度還是重新置為其他值）

•影像的邊緣，也就是遮罩會有部分超出影像的地方該怎麼辦?

忽略邊緣

補零

鏡射

04362782 柯岱佑 HW04

空間濾波
現在美肌APP，或是一些濾鏡基本上用到的都是空間濾波的概念，人工智慧裡CNN也是透過類似的概念去抓取影像中的特徵點來做運算，以下會介紹最基本的三種濾波。

原理是我們透過一個基數的方陣3*3、5*5之類的將你要修改的象素點放在中間位置，你就會獲得這個點的色彩值與他周圍象素的色彩值在根據這些值去做修改。

Smoothing Filter(平滑濾波器)
我們給九個點對應的權重，再把他們相加，最後平均這樣它的色彩值就會更趨近於鄰近的色彩值，當色彩值相近就會使色差減少形成一個柔化的效果。

 胡椒鹽與中值濾波器(Median Filter and Pepper-and-salt Noise)

以前的相機當你把ISO值調太高的時候很容易就會有雜訊跑出來，一點一點的跟胡椒鹽一樣，所以我們把它稱為胡椒鹽雜訊，而中值濾波器可以幫助我們把胡椒鹽雜訊消除掉，那他要做的方法是把極端的值給排除掉，那他會把抓到的九個點逕行排列然後取中位數，基本上極端的都會出現在兩側所以可以透過這樣把它個替換掉，但這樣也出現了一點柔化的效果，因為她也不是原本的值他只是找了一個相近的值來替換他而已。

胡椒鹽雜訊

經過中值濾波器處裡後

銳化濾波器(sharp filter)

當我們照相時些微的顫抖照成了照片有點模糊時，銳化濾波器可以幫我們呈現一個較清晰的影像，那他會用到一些微積分，拉普拉斯轉換我也看不太懂為甚麼要這樣做，但最後減化出來的公式，大概了解到我們給予中間點即高的權重，讓他減去周圍的點，剩下的值一定比原來的值高或低，與周圍個治的差也會變大，因此加強了色差，形成了較強的對比度讓畫面更佳的顆粒。

原圖

寫這份作業遇到的問題是imageRowInitialPosition = (unsigned char *)Image1->Picture->Bitmap->ScanLine[i];這個東西一次只抓一列得色彩值要處理這個要嘛一次抓三列，但感覺很麻煩所以我創了3個陣列把RGB各至丟進去，再創3個陣列去裝銳化後的值因為，只用一組的化再改動時會改到原來的值，這樣下一個值就不是依原圖來做銳化處裡了，所以總共6個陣列，但當圖太大時C++ Builder會說 Stack Overflow 所以你必須用動態宣告他把空間創在heap，然後再做銳化得時候得到的值有可能小於0或大於255要記得處裡一下不然圖片會出現奇怪象素點。

03361204 王甯 HW4

空間濾波

概要

　　在第一次聽到濾波器的時候，其實我並不了解波與影像之間的關係，在上完課之後才理解它其實是類似函數的概念，在圖片中的像素（光）到達眼睛之前，進行過濾。

心得

3x3濾波器

　　課堂中介紹的濾波器如上圖，使用時可以想像成是將濾波器覆蓋在圖片上的9個像素，然後重新計算中間那個像素。計算方法也很直觀，將圖中的每個像素與對應的濾波器係數w(x,y)相乘，最後再相加即可。如果將計算後中間那格記作g(x,y)，原圖的像素記作f(x,y)，則有一個簡易的公式：

濾波器計算公式

根據功能的不同，又分成：

　　1. 平滑濾波器：將移除圖片中的小細節，讓圖片變得比較平滑，過度使用的話則會變得模糊。

原圖

使用3x3平滑濾波器後的結果

　　2. 中值濾波器：將移除圖片中的極值，也就是消除極端雜訊。

　　3. 銳化濾波器：與平滑濾波器恰巧相反，用於凸顯細節、強化差異。

　　　　　　　　　　　　　原圖　　　　　　　　使用銳化濾波器

04362411 王偉橋,HW04

空間濾波

空間濾波是用一個九宮格的遮罩,然後通過公式轉換改變中間那個色彩值,從而產生新的圖像

.

平滑空間濾波器(Smoothing Spatial Filter)

平滑濾波器的主要用途是模糊化和減少雜訊,方法就是將中間那個的色彩值改為九宮格的平均值.遮著如下:

平滑遮罩

範例圖片依舊是lena

原圖

平滑濾波器

平滑濾波器後圖片有稍微變得模糊.

銳化濾波器

銳化濾波器能夠更加凸顯圖片的細節,以及色彩強度的變化,還能夠使圖片的線條感更加明顯,運用二階導數,是因為二階導數在影像的細節處理上,比一階導數更加好用,銳化的遮罩是通過拉普拉斯轉化得到的,通過整理後的遮罩如下:

銳化遮罩

經過銳化處理後的圖片為:

銳化濾波 

濾波器還有一個中值的,他就是中間的色彩值改為將遮罩中的中位數,經常會用在處理胡椒鹽的圖片上處理雜訊.

04360286 趙俊彥,HW04

平滑空間濾波，用來模糊化圖片以及減少雜訊

以這張圖片來舉例，我將圖片內的像素以九宮格為一組，將其像素點的RGB相加起來得到一個總和，再將其除九後得到九宮格內的平均值再將其放回這一組像素點的RGB就會得到以下這張圖片

雖然不是很明顯，但可以看的出來確實有比較模糊一點

胡椒鹽雜訊
將圖片遍循每一個像素點的同時去計算亂數，將5以下的亂數的像素點設為白色，即可得到5%胡椒鹽雜訊圖，以此類推想要幾%就將多少以下的亂數的像素點設為白色即可

這樣的胡椒鹽雜訊圖我們可以使用中值濾波器來取得與原圖極為相識的圖片，一樣以九宮格為一組，將所有像素點的顏色記錄起來後取中值，即可將偏差較大的值去掉

銳化，一樣是以九宮格為一組，特別強調中央的值，來達到銳化的效果，將九宮格的像素點的值都加起來後，再加上中央的像素點的值*-9，再用中央像素點的值去-掉這個總和，這樣就可以得出特別強調中央的像素點的值了，要注意的是，這個值指放入中央的這個像素點，其旁邊的像素點也有其九宮格

03362421 林謙 HW04

空间滤波 Spatial Filtering

03362421 林謙

空間濾波是圖像處理中的一個基本操作，用一個適合的濾波器，就能讓圖像變得平滑或者銳化，甚至可以去除噪點。

下圖是卷積的操作，只不過和濾波的區別不大，濾波只是在最外一圈補上0讓最後的大小和原圖一樣大而已。

我認為通過看這個gif比通過看枯燥的公式更加能讓我理解什麼是濾波，濾波到底在做什麼。

卷積示例

下面我做的示例都會將在同一張原圖上，依舊是我很喜歡的電影“Carol”的電影劇照

Carol劇照
未經處理的原圖

如果濾波器的各項和大於1，那麼畫面就會比原來的量，如果等於1，亮度就不會變化，如果小於1，那麼畫面就會變得比較暗。

平滑濾波器

1	1	1
1	1	1
1	1	1

當然在使用這個濾波器的時候， 最後的結果要除以9 

進過平滑濾波的劇照

銳利濾波器

0	-1	0
-1	5	-1
0	-1	0

經過銳利處理好后的劇照

高斯濾波器

高斯模糊，也可以通過濾波器來做到

1	4	7	4	1
4	16	26	16	4
7	26	41	26	7
4	16	26	16	4
1	4	7	4	1

當然，在用這個濾波器的時候最後要除以273

高斯模糊后的劇照

空間濾波還有更多的應用，但是篇幅關係，這裡就不再多介紹了。

04360526 陳亮廷 HW04

平滑與中值和銳化濾波器

這次的作業是對影像加上濾波處理，分別有對影像色彩值取平均的平滑濾波器、對影像色彩值取中值的中值濾波器，還有利用微分來增加色彩值差異的銳化濾波器。

程式部份我是使用BCB6來製作:

平滑濾波器:

使用前:

使用後:

因為平滑濾波器是將單格的色彩值，改成自己與它周圍九格的色彩值平均，所以該格的色彩值會變得較為接近它周圍格子的色彩值，也就是彼此的色彩值差異變小，所以照片自然會變得較為模糊。

使用五次後:

可以看到圖片比上一張變得更為模糊了，因為每次都會對色彩值取平均，因此相鄰格子的色彩值會越來越接近。

中值濾波器:

有請乾淨漂亮的荷包蛋現身:

中值濾波器的應用為處理雜訊，因為雜訊通常都為極值，若對

9個格子的色彩值取中值，就可以將雜訊處理掉，順帶選擇較為接近鄰近格子的色彩值。

撒上5%的胡椒鹽雜訊:

中值濾波後:

可以看到雜訊消失了，基本上整張圖片的雜訊是可以被清理的。

撒上20%的胡椒鹽雜訊:

中值濾波後:

可以看到跟5%的雜訊經過中值處理後相比，雜訊明顯的變多了，因為20%的雜訊較為密集，黑點或白點擠在一起的機率較高，在一群黑點中取中值還是會是黑點。

銳化濾波:

使用前:

使用後:

可以看出月球上的凹凸更為明顯，原本較為接近灰色的部分也變得較為明亮了，因為彼此的特徵差異變的巨大，銳化濾波器的應用就是將照片變得清楚。

到這裡可以發現，銳化與平滑濾波剛好是做相反的事，銳化是將影像變得清楚，平滑卻會將影像變得模糊，銳化是利用微分將色彩值的差異突顯出來，平滑則是利用平均將色彩值變得接近，微分與積分是一對的，而積分也可以用來算平均，只是用來算連續函數的，那麼是不是對頻率域連續函數是否可以利用積分來獲得跟中值濾波一樣的效果呢?