Affine Transformation
This program facilitates the application of the affine transformation to a 2-D Image.
看完了這段英文...我想這段英文寫的意思是:
這段程式,幫助2D影像仿射轉換的運用。
MATLAB網站:
http://www.mathworks.com/matlabcentral/fileexchange/3025
而所謂的「Affine Transformation (仿射轉換)」就是將影像坐標(Sample, Line)轉換成像坐標(x,y)。
-------------------------------------------------------------------------------------
Chapter 6:Image Geometry
開頭的那段寫著:
有很多的情況,我們可能想要去改變影像的形狀、大小或方位。
我們可能想要去擴大影像去適合特定的空間或印刷;
也可能想要去縮小它的尺寸,包括在網頁上。
我們可能希望去旋轉它,可能對不合適的相機角度做調整,或單純地為了效果。
旋轉和比率(大小)是仿射轉換的例子,線條轉換成線條,尤其是平行線在轉換之後保持平行。
非仿射的幾合轉換包含彎曲,但我們經常沒有把它考慮在這裡。
這段大概就是做初步的帶入,但我真的看不太懂倒數第二行的線條轉換成線條是什麼意思@@"
6.1 Interpolation of Data
Start with a simple problem:
suppose we have a collection of four values that we wish to enlarge to eight.
「如何把四個數字擴大八個數字?」
課本上提到了三種方法:
1)Slightly redrawn
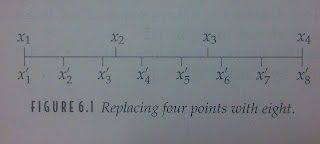
X1 ~ X4 之間一共有三個間隔,而每個間隔相差的直為1,
X'1 ~ X'8 的長度與 X1~X4的長度相等,X'1 ~ X'8之間一共有七個間隔(如上圖6.1所示),
所以每個間隔的大小為3/7 大約等於0.4286。
數學公式如下:
X'=1/3(7x-4)
X =1/7(3x'+4)
將等長度由四等份分為八等份,故每段長度變小(如下圖6.2所示)。

2)Nearest-neighbor interpolation
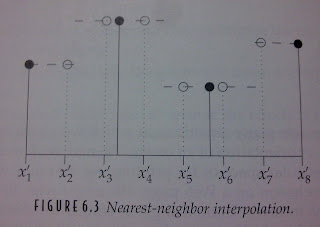
X →X' 挑最近的的點,如上圖6.3所示:
X1最近的點:X'1 & X'2 (X'2標空圈)
X2最近的點:X'3 & X'4
X3最近的點:X'5 & X'6
X4最近的點:X'7 & X'8 (X'7標空圈)
3)Linear interpolation
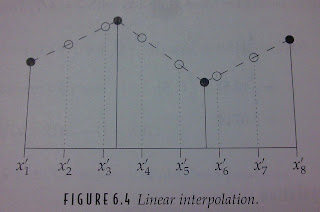
主要是將X1與X2連線,取X'2對應到線上的點為X'2(X'2標空圈),以此類推。
而要計算linearly interpolated values,一定要為線型。
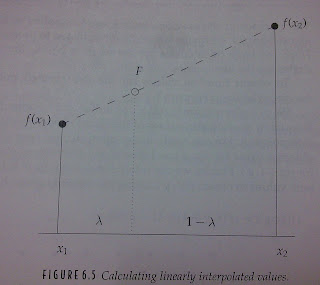
數學原理為:
〔F-f(X)〕/λ = 〔f(X2)-f(X1)〕/1
→F=λf(X2)+(1-λ)f(X1)
註:F是想知道的X'n
λ是以 X1 到 X2 的距離,F距離 X1 佔整段比例的比數
6.2 Image Interpolation
在6.1提到了點與線之間的數值放大(使用線性做範例),
而在此6.2則是討論一個面的,也就是Image。
例如:將4×4的Image放大到8×8,
(x,y)對應到放大後的位置,用下面的公式計算,
則該公式稱為 bilinear interpolation。
f(x',y')=λ〔μf(x+1,y+1)+(1-μ)f(x+1,y)〕
+(1-λ)〔μf(x,y+1)+(1-μ)f(x,y)〕
=λμf(x+1,y+1)+λ(1-μ)f(x+1,y)
+(1-λ)μf(x,y+1)+(1-λ)(1-μ)f(x,y)
上面最後的方程式為bulinear interpolation的公式。
Matlab內有個 function 叫做 imresize,負責上述提過的處理,
它的語法是:imresize(A, k, 'method')
A是任何型態的影像,K是比率係數,
而method是 "nearest" 或 "'bilinear" 二者之中任一個。
另一種imresize的語法則是:
imresize(A, [m,n] , 'method')
[m,n] 則表示輸出的比率大小。
下面是課本上的程式碼:
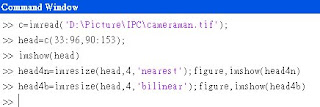
而下面則是nearest和bilinear的比較:
下圖為bicubic

而下圖為nearest neighbor

根據二張圖的推判,得知用nearest內插法誤差大於用bilinear內插法!
6.3 General Interpolation
一開始我們希望把 x' 插在 x1 ≤ x' ≤ x2 之間,並假設 x' - x1 = λ。
然後定義一個interpolation function R(u)且 f(x') = R(-λ)f(x1) + R(1-λ)f(x2)。
利用三種函數方程式表示6.2所示的方法
(1)Nearest-neighbor interpolation
{0 if u≦-0.5
R0(u)={1 if -0.5<u≦0.5
{0 if u>0.5
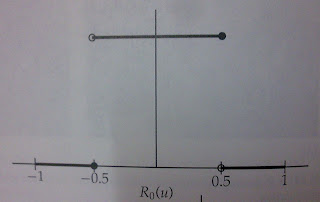
(2)Linear interpolation
R1(u)={1+u if u≦0
{1-u if u≧0
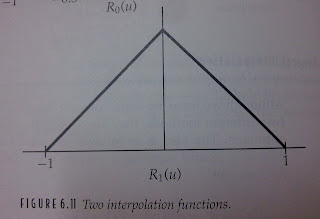
(3)Cubic interpolation
也就是Method中的bicubic....
因為計算的過程中該曲線f(x)的x值,最高項次是 3次方,
而且,在平面上求得(x',y')需仰賴bilinear的概念
所以稱為bicubic interpolation。
R3(u)={1.5∣u∣^3-2.5∣u∣^2+1, if ∣u∣≦1,
{-0.5∣u∣^3+2.5∣u∣^2-4∣u∣+2 if 1<∣u∣≦2
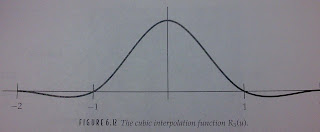
6.4 Enlargement by Spatial Filtering
如果只是要將圖放大兩倍, 有個快速且糟糕的方法就是使用linear filtering。
step1.對這個矩陣做zero-interleave,即在原行列之間加零。

step2.做filtering。
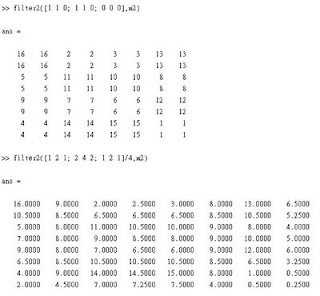
6.5 Scaling Smaller
讓Image變比較小,也稱為Image minimization,
有一種方法是刪除間隔的pixel值,稱為subsampling,
它符合 imresize 的 nearest,是一種非常簡單的手段,但對高頻的部分效果不佳。
(是因為相近的pixel值差很多,但這些相近的pixel都被刪除了嗎?????)
沒有留言:
張貼留言