p181 中的homfilt的function定義中的hb_butter(im,utoff,order,lowgain,highgain)是做什麼動作?且我在執行時他說沒有定義此function。
p171 中的[x,y]=meshgrid(-128:127,-128:127);z=sqrt(x.^2+y.^2);c=(z>15);為甚麼此舉可以產生圓形?其中的z=sqrt(x.^2+y.^2);不是畢氏定理嗎?而且我產生的c為甚麼內容皆為1?
這次因為我有事所以先回家了~這次的課沒到．再這次發問題順便跟老師請個假．
2007年12月27日 星期四
2007年12月26日 星期三
Week15
閱讀心得:
根據老師上次上課的解說重新把前面的再看一次.重新釐清一些觀念.一維離散傅立葉轉換:
F = Ff
f=[f0,f1,f2,...,fn-1]
F=[F0,F1,F2,....,FN-1] , F是各個波形的係數值
F是組成的各個波形
二維的根一維的很相似,差別在於一維的是線性的二維的是平面的
我們所知道的圖片都是由二維組成的圖片中的每一點都可以表示成(x,y)
問題:
p156
最後一段他說Equation 7.4 和 7.5 最主要的差別就是 7.5多了 1/MN 位置座標因素,
有些人則在放1/√MN ,而在前面乘於 1/MN 和 1/√MN 有甚麼差別嗎?
p158 Figure 7.6 是否是表示再處理二維的DFT,事先將所有的Row都處理完之後再處理所有的
Column或著 先處理所有的Column在所有的Row在,而不是一個pixel一個pixel去做處理.
p159 d= f + n 式子中n是表示在做傅立葉轉換會有干擾這些干擾會使圖片成為被降級的圖片,而n也就是所謂的干擾是甚麼??
f=[f0,f1,f2,...,fn-1]
F=[F0,F1,F2,....,FN-1] , F是各個波形的係數值
F是組成的各個波形
二維的根一維的很相似,差別在於一維的是線性的二維的是平面的
我們所知道的圖片都是由二維組成的圖片中的每一點都可以表示成(x,y)
問題:
p156
最後一段他說Equation 7.4 和 7.5 最主要的差別就是 7.5多了 1/MN 位置座標因素,
有些人則在放1/√MN ,而在前面乘於 1/MN 和 1/√MN 有甚麼差別嗎?
p158 Figure 7.6 是否是表示再處理二維的DFT,事先將所有的Row都處理完之後再處理所有的
Column或著 先處理所有的Column在所有的Row在,而不是一個pixel一個pixel去做處理.
p159 d= f + n 式子中n是表示在做傅立葉轉換會有干擾這些干擾會使圖片成為被降級的圖片,而n也就是所謂的干擾是甚麼??
2007年12月25日 星期二
Week 15 - Chapter 7 THE FOURIER TRANSFORM
◈ 主題 :
INTRODUCTION TO DIGITAL IMAGEPROCESSING
Chapter 7: THE FOURIER TRANSFORM
◈ 詳細閱讀
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 實作心得 :
(工事中...)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 問題 :
① Page 143 第三、四句話／Introduction
｢its efficiency allows us to perform other task more quickly.｣，為什麼要說other task?前面並沒有寫什麼任務，那麼又是哪來的其他任務?
｢The Fourier transform provides, among other things, a powerful alternative to linear spatial filtering.｣，為什麼要說other things?前面並沒有寫什麼事，那麼又是哪來的其他事?
② Page 148 算完ω後算的那個F／DFT
根據這一頁的最上面，矩陣前面有個1/N，所以這裡是不是少寫了1/4。
Ans：這裡確實少了1/4。[已解決]
③ Page 152 z3下面的第一、二句話／convolution
不知道negative indices是指什麼，不知道為什麼會有這樣的等式關係，不知道這個等式關係想表達什麼。
④ Page 157 這一段倒數第三行／THE DFT AS A SPATIAL FILTER
處理edge問題的時候，｢We assume that the image is tiled in all directions so that the mask always has image values to use.｣，不知道這句話是什麼意思，為什麼這樣就沒有edge問題了。
⑤ Page 161 FIGURE7.8／CONJUGATE SYMMETRY
上下左右對稱，為什麼b、d沒有像A、B一樣左右互換而只有上下互換。
⑥ Page 161 第二句／CONJUGATE SYMMETRY
為什麼要讓u=-u，v=-v，不知道這樣與CONJUGATE SYMMETRY有什麼關係。
⑦ Page 164 上半部最後一句／Example
是剛好這個single edge的矩陣做DFT後得到的DC係數shift後剛好有鏡射的效果於是就提到了DFT的對稱?
⑧ Page 163 Example7.6.3／Example
不知道single-step edge是什麼(註:後面章節也有稱為single edge的)。這種左半為零右半為一的矩陣就稱為single edge?
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 備註 :
前兩週有失以往的專心度導致很多地方沒看清楚，這週從頭開始閱讀，目
前閱讀完7.1~7.7，會再找時間盡快閱讀完剩下的7.8、7.9。上一週提出
的問題會在全部閱讀完後與統整至本週問題。
INTRODUCTION TO DIGITAL IMAGEPROCESSING
Chapter 7: THE FOURIER TRANSFORM
◈ 詳細閱讀
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 實作心得 :
(工事中...)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 問題 :
① Page 143 第三、四句話／Introduction
｢its efficiency allows us to perform other task more quickly.｣，為什麼要說other task?前面並沒有寫什麼任務，那麼又是哪來的其他任務?
｢The Fourier transform provides, among other things, a powerful alternative to linear spatial filtering.｣，為什麼要說other things?前面並沒有寫什麼事，那麼又是哪來的其他事?
② Page 148 算完ω後算的那個F／DFT
根據這一頁的最上面，矩陣前面有個1/N，所以這裡是不是少寫了1/4。
Ans：這裡確實少了1/4。[已解決]
③ Page 152 z3下面的第一、二句話／convolution
不知道negative indices是指什麼，不知道為什麼會有這樣的等式關係，不知道這個等式關係想表達什麼。
④ Page 157 這一段倒數第三行／THE DFT AS A SPATIAL FILTER
處理edge問題的時候，｢We assume that the image is tiled in all directions so that the mask always has image values to use.｣，不知道這句話是什麼意思，為什麼這樣就沒有edge問題了。
⑤ Page 161 FIGURE7.8／CONJUGATE SYMMETRY
上下左右對稱，為什麼b、d沒有像A、B一樣左右互換而只有上下互換。
⑥ Page 161 第二句／CONJUGATE SYMMETRY
為什麼要讓u=-u，v=-v，不知道這樣與CONJUGATE SYMMETRY有什麼關係。
⑦ Page 164 上半部最後一句／Example
是剛好這個single edge的矩陣做DFT後得到的DC係數shift後剛好有鏡射的效果於是就提到了DFT的對稱?
⑧ Page 163 Example7.6.3／Example
不知道single-step edge是什麼(註:後面章節也有稱為single edge的)。這種左半為零右半為一的矩陣就稱為single edge?
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 備註 :
前兩週有失以往的專心度導致很多地方沒看清楚，這週從頭開始閱讀，目
前閱讀完7.1~7.7，會再找時間盡快閱讀完剩下的7.8、7.9。上一週提出
的問題會在全部閱讀完後與統整至本週問題。
2007年12月20日 星期四
week14
因為我是是用彩色的故在mask上面需要做三次，原先要使用mod去運算，但是會出錯只好分別的做三次for。
a=imread('untitled.jpg');
b=imread('10.jpg');
a=imresize(a,[300 300]);
b=imresize(b,[300 300]);
mask=imread('untitled.jpg');
mask=imresize(mask,[300 300]);
mask1=zeros(300);
for(i=1:150)
mask1(i:301-i,i:301-i)=i/128;
end
for i=1:300
for j=1:300
mask(i,j)=(mask1(i,j)*a(i,j)+(1-mask1(i,j))*b(i,j));
end
end
for i=1:300
for j=301:600
mask(i,j)=(mask1(i,j-300)*a(i,j)+(1-mask1(i,j-300))*b(i,j));
end
end
for i=1:300
for j=601:900
mask(i,j)=(mask1(i,j-600)*a(i,j)+(1-mask1(i,j-600))*b(i,j));
end
end
imshow(mask)
week14 CH7
1.fft(a')中的 ' ,是什麼意思?
有加跟沒加的結果有差, 但似乎又只是排列方法不同而已.. P.149
2.temp([a a],b)算出來的值為什麼會和p(u)q(u)(1-u^4)算出來的係數一樣? P.153
這禮拜還是看不多, 一樣是跳著看跳著看,
有些東西還是很難理解
例: fft , ifft , fft2... 等
不懂為什麼顯示出來是這樣
課堂上:
x=imread('111.TIF');
y=imread('222.TIF');
for i=1:128,
mask(i:257-i,i:257-i)=i/128;
end
x1=rgb2gray(x);
y1=rgb2gray(y);
x2=mat2gray(x1);
y2=mat2gray(y1);
z=x2.*(1-mask)+y2.*mask;
imshow(z)
有加跟沒加的結果有差, 但似乎又只是排列方法不同而已.. P.149
2.temp([a a],b)算出來的值為什麼會和p(u)q(u)(1-u^4)算出來的係數一樣? P.153
這禮拜還是看不多, 一樣是跳著看跳著看,
有些東西還是很難理解
例: fft , ifft , fft2... 等
不懂為什麼顯示出來是這樣
課堂上:
x=imread('111.TIF');
y=imread('222.TIF');
for i=1:128,
mask(i:257-i,i:257-i)=i/128;
end
x1=rgb2gray(x);
y1=rgb2gray(y);
x2=mat2gray(x1);
y2=mat2gray(y1);
z=x2.*(1-mask)+y2.*mask;
imshow(z)
Chapter 7
Chapter 7閱讀至今，仍然以緩慢的速度進行
在post這篇blog的當下，進度只到Page 168而已
(其中Page 151-162 僅僅粗略的閱讀)
(晚點若有更多進度，持續更新)
《閱讀心得》
傅立葉轉換，由於課本的進行方式是以數學公式與圖例來講解，這不是我所擅長的理解類型，因此在一開始的時候以查閱wiki百科上的內容為主；傅立葉轉換可分為：離散、連續、一階、多階等形態。每種型態各有其用途與立意，課本於 7.3 (Page146)時提到了離散傅立葉轉換(DFT)，而wiki百科提到了"離散傅立葉轉換後，頻率域仍連續"的特性，開始思索這與影像處理的關聯性。
猶記得印象中，一張圖片的資訊可分為：頻率域與空間域。
課本於Page 160提到了DC coefficient就是頻率域裡的係數。
傅立葉轉換做為Filter的用途上，似乎可以簡單且多樣化的Filtering，然而對於傅立葉轉換仍不是很了解，wiki百科上提到"信號處理中，富立葉轉換的典型用途是將信號分解成幅值分量和頻率分量"。(希望老師能撥空將這方面的知識作講解 "空間域v.s.頻率域"＆"頻率域v.s.傅立葉轉換")
《問題區》
1. 照著課本指令打，雖然run的結果與課本一樣，然而指令的實際用途卻不是很能理解..像是fft2這類的。
2. 見"閱讀心得"，"空間域v.s.頻率域"＆"頻率域v.s.傅立葉轉換"，希望能知道這方面的知識，雖然不知道提出這個問題是否與課堂有關。
在post這篇blog的當下，進度只到Page 168而已
(其中Page 151-162 僅僅粗略的閱讀)
(晚點若有更多進度，持續更新)
《閱讀心得》
傅立葉轉換，由於課本的進行方式是以數學公式與圖例來講解，這不是我所擅長的理解類型，因此在一開始的時候以查閱wiki百科上的內容為主；傅立葉轉換可分為：離散、連續、一階、多階等形態。每種型態各有其用途與立意，課本於 7.3 (Page146)時提到了離散傅立葉轉換(DFT)，而wiki百科提到了"離散傅立葉轉換後，頻率域仍連續"的特性，開始思索這與影像處理的關聯性。
猶記得印象中，一張圖片的資訊可分為：頻率域與空間域。
課本於Page 160提到了DC coefficient就是頻率域裡的係數。
傅立葉轉換做為Filter的用途上，似乎可以簡單且多樣化的Filtering，然而對於傅立葉轉換仍不是很了解，wiki百科上提到"信號處理中，富立葉轉換的典型用途是將信號分解成幅值分量和頻率分量"。(希望老師能撥空將這方面的知識作講解 "空間域v.s.頻率域"＆"頻率域v.s.傅立葉轉換")
《問題區》
1. 照著課本指令打，雖然run的結果與課本一樣，然而指令的實際用途卻不是很能理解..像是fft2這類的。
2. 見"閱讀心得"，"空間域v.s.頻率域"＆"頻率域v.s.傅立葉轉換"，希望能知道這方面的知識，雖然不知道提出這個問題是否與課堂有關。
week14 Ch7
我去網路上找了有關Fourier 轉換的資訊 , 大概簡單的統整出下列:
1.Fourier 轉換能把任意的時域( time domain )函數以數學方法轉換成頻域( frequency domain )函數，包括周期性函數與非週期性函數皆可.
2.幾乎所有理工科系的學生都會遇到處理訊號的問題，尤其是電機、電子科系的學生，更有一門專門的課叫「數位訊號處理」，也有一門比較屬於入門的課叫「訊號與系統」，皆會討論到訊號，包括如何以數學描述訊號、分類、處理、頻域與時域的特性等等，而最常用的數學技巧就是 Fourier 轉換.
3.Fourier 轉換的數學定義為：F{ ƒ(t) }≡∫ƒ(t)e-jωtdt = F(ω) , 積分範圍：- ∞ ～ ∞
Fourier 轉換就是將時域函數( 訊號 ) ƒ(t) 乘上 e-jωt 然後對時間 t 做積分，積分範圍從負無限大到正無限大，積分出來的結果就是頻域函數 F(ω).
4.在 Fourier 轉換中，ω 通常表示為角頻率( angle frequency )，即：
ω = 2πƒ.
1.Fourier 轉換能把任意的時域( time domain )函數以數學方法轉換成頻域( frequency domain )函數，包括周期性函數與非週期性函數皆可.
2.幾乎所有理工科系的學生都會遇到處理訊號的問題，尤其是電機、電子科系的學生，更有一門專門的課叫「數位訊號處理」，也有一門比較屬於入門的課叫「訊號與系統」，皆會討論到訊號，包括如何以數學描述訊號、分類、處理、頻域與時域的特性等等，而最常用的數學技巧就是 Fourier 轉換.
3.Fourier 轉換的數學定義為：F{ ƒ(t) }≡∫ƒ(t)e-jωtdt = F(ω) , 積分範圍：- ∞ ～ ∞
Fourier 轉換就是將時域函數( 訊號 ) ƒ(t) 乘上 e-jωt 然後對時間 t 做積分，積分範圍從負無限大到正無限大，積分出來的結果就是頻域函數 F(ω).
4.在 Fourier 轉換中，ω 通常表示為角頻率( angle frequency )，即：
ω = 2πƒ.
Week14-CH07
在p.174的第二數學式子m, n為什麼可以取代x和u？
m和n是代表矩陣中的x和y麼？
在7.3中說的是一維傅立葉轉換，可是矩陣不是二維？怎麼叫做一維啊？
在7.4的程式中，我沒有辦法算出x1，x1像是把x翻轉過來一樣的規律，我也沒有辦法從上面的數學
式子中倒出這種關係
然後這一章中大部分的數學算式，我都沒辦法倒出來，或者是沒有辦法從前面的算式倒到下一個
算式
7.5應該說的是傅立葉轉換的性質；對稱性和周期性，我是看網路資料的，但是還是看不太懂數學
式反映在圖形上的方法
先這樣
m和n是代表矩陣中的x和y麼？
在7.3中說的是一維傅立葉轉換，可是矩陣不是二維？怎麼叫做一維啊？
在7.4的程式中，我沒有辦法算出x1，x1像是把x翻轉過來一樣的規律，我也沒有辦法從上面的數學
式子中倒出這種關係
然後這一章中大部分的數學算式，我都沒辦法倒出來，或者是沒有辦法從前面的算式倒到下一個
算式
7.5應該說的是傅立葉轉換的性質；對稱性和周期性，我是看網路資料的，但是還是看不太懂數學
式反映在圖形上的方法
先這樣
week14_CH7
1)page 149
fft()的結果是求得傅立葉轉換前的transform,為什麼6個數經fft是產生相加的和與5個數?
2)page 151
conjugate是共軛? 為什麼第k個會和N-k的共軛值相等?
3)page 152
p(u)q(u)(1+u^N)和z=x*y有什麼關係?
fft()的結果是求得傅立葉轉換前的transform,為什麼6個數經fft是產生相加的和與5個數?
2)page 151
conjugate是共軛? 為什麼第k個會和N-k的共軛值相等?
3)page 152
p(u)q(u)(1+u^N)和z=x*y有什麼關係?
Week13 - CHAPTER 7
「離散傅立葉轉換」（Discrete Fourier Transform）簡稱 DFT，其功能是將一段數位訊號轉換成其各個頻率的正弦波分量。如果我們的訊號可以表示成 x[n], n = 0~N-1，那麼 DFT 的公式如下：
X[k]=(1/N)*Sn=0N-1 x[n]*exp(-j*2p*n*k/N), k=0, ..., N-1
這些傅立葉係數 X[k] 所代表的資訊是 k 的函數，而 k 直接和頻率有正比關係，因此這些係數 X[k] 通稱為「頻譜」（Spectrum），而對於 X[k] 的分析，我們通稱為「頻譜分析」（Spectral Analysis）。我們也可以由這些傅立葉係數 X[k]，來反推原始訊號 x[n]，如下：
x[n]=Sk=0N-1 X[k]*exp(j*2p*n*k/N), n=0, ..., N-1
而Fourier轉換是頻譜儀的數學基礎，把一個時域信號（不管週期或非週期的）輸入至頻譜儀，輸出畫面可能會顯示出數個只有表示振幅大小與頻率的信號；若一開始輸入三角波，轉換後並不會是三角波，轉換後的波形可用頻譜儀看，或自己計算出結果用數學分析軟體Matlab來模擬。
1. t = 0:19;
2. x = sin(2*pi*t/5)+2*cos(2*pi*t/10);
3. plot(t,x);
4. xfft = fft(x);
5. figure;
6. plot(abs(xfft),'*');
透過實驗後，知道上述的功能
1. t = 0:19;
->t 從1到19
2. x = sin(2*pi*t/5)+2*cos(2*pi*t/10);
->定義x這個函數 x是t的函數
3. plot(t,x);
-> 把這個函數畫出來 因為之前定義t是從1到19， 所以這個函數只繪畫出從1到19這一段
4. xfft = fft(x);
-> 對x這個函數做快速傅立葉轉換 結果存到xfft
5. figure;
->再開一個繪圖框
6. plot(abs(xfft),'*');
->畫出 xfft的絕對值 用*畫出來
以上是這禮拜閱讀的心得，主要在了解傅立葉到底是什麼東西
以及如何去使用它
而Fourier轉換是頻譜儀的數學基礎，把一個時域信號（不管週期或非週期的）輸入至頻譜儀，輸出畫面可能會顯示出數個只有表示振幅大小與頻率的信號；若一開始輸入三角波，轉換後並不會是三角波，轉換後的波形可用頻譜儀看，或自己計算出結果用數學分析軟體Matlab來模擬。
1. t = 0:19;
2. x = sin(2*pi*t/5)+2*cos(2*pi*t/10);
3. plot(t,x);
4. xfft = fft(x);
5. figure;
6. plot(abs(xfft),'*');
透過實驗後，知道上述的功能
1. t = 0:19;
->t 從1到19
2. x = sin(2*pi*t/5)+2*cos(2*pi*t/10);
->定義x這個函數 x是t的函數
3. plot(t,x);
-> 把這個函數畫出來 因為之前定義t是從1到19， 所以這個函數只繪畫出從1到19這一段
4. xfft = fft(x);
-> 對x這個函數做快速傅立葉轉換 結果存到xfft
5. figure;
->再開一個繪圖框
6. plot(abs(xfft),'*');
->畫出 xfft的絕對值 用*畫出來
以上是這禮拜閱讀的心得，主要在了解傅立葉到底是什麼東西
以及如何去使用它
Week14 Ch_7 THE FOURIER TRANSFORM
(1)更改掉錯誤了~跟課本一樣!
(2)課本裡的fft2二維離散傅立葉轉換，我試過課本裡的幾個例子，但是就是弄不懂裡面的值怎麼產生的? 如果是fft衍伸過來的算法，那是怎麼算的，因為在7-5那講的Two-Dimensional DFT就看的有點模糊了。 fft2(X) can be simply computed as fft(fft(X).').' 他意思是不是說二維傅立葉轉換為先對行或列進行一維傅立葉轉換後，再對列或行進行一維傅立葉轉換的結果。
心得: 因為在二維那邊就卡住了，後面我看了一下，還頗有關係的，目前繼續了解它中....@@
Week14 Ch7 Reading
我自己的方法
c=ones(300,300);
temp=ones(299,299);
d=filter2(temp,c);
d=d-22500;
d=d/66901;
上次上課的方法建立MASK矩陣
mask=zeros(300);
for i=1:150,
mask(i:301-i,i:301-i)=i/150;
結果出來後發現我的方法建立出來的矩陣周圍偏高
所以效果較不明顯
我自己的
老師的
----------------------------------------------------
回家後繼續完成上次的考試 不過我建立矩陣的方法沒有像黃老師上課所說不太一樣
不過建立出來的矩陣則是差不多
第7張好像都是在說如何利用傅利葉來處裡圖片並顯示其傅利葉轉換的結果
因為可能是微積分被當一套的..所以式子方面讀起來有點困難...
不過老師上禮拜有大概說一點東西 所以可以知道他最基本的東西吧
不太了解P165那種轉換的原理然後取對數或者取絕對直的轉換
也許是跳著看..漏了一點..會再往前補上.之後再來研究
c=ones(300,300);
temp=ones(299,299);
d=filter2(temp,c);
d=d-22500;
d=d/66901;
上次上課的方法建立MASK矩陣
mask=zeros(300);
for i=1:150,
mask(i:301-i,i:301-i)=i/150;
結果出來後發現我的方法建立出來的矩陣周圍偏高
所以效果較不明顯
我自己的
老師的
----------------------------------------------------
回家後繼續完成上次的考試 不過我建立矩陣的方法沒有像黃老師上課所說不太一樣
不過建立出來的矩陣則是差不多
第7張好像都是在說如何利用傅利葉來處裡圖片並顯示其傅利葉轉換的結果
因為可能是微積分被當一套的..所以式子方面讀起來有點困難...
不過老師上禮拜有大概說一點東西 所以可以知道他最基本的東西吧
不太了解P165那種轉換的原理然後取對數或者取絕對直的轉換
也許是跳著看..漏了一點..會再往前補上.之後再來研究
Week14 CH7 Read
將上次考試的合成圖，運用老師所說的遮罩(mask)方法再做一遍，
得到下圖 (.m)檔案如下!
---------------------------------------
a=imread('ic.tif');
b=imread('blocks.tif');
mask=zeros(256);
for i=1:128,
mask(i:257-i,i:257-i)=i/128;
end
g=mat2gray(a);
k=mat2gray(b);
c=g.*(1-mask)+k.*mask;
imshow(c);
---------------------------------------
感覺不錯，省掉許多麻煩的步驟。
第七章問題︰
許多公式不解其推導...
DFT部分也蠻模糊的...
figure 7.28 Low - pass filtering 和 High - pass filtering 指的是什麼?
得到下圖 (.m)檔案如下!
---------------------------------------
a=imread('ic.tif');
b=imread('blocks.tif');
mask=zeros(256);
for i=1:128,
mask(i:257-i,i:257-i)=i/128;
end
g=mat2gray(a);
k=mat2gray(b);
c=g.*(1-mask)+k.*mask;
imshow(c);
---------------------------------------
感覺不錯，省掉許多麻煩的步驟。
第七章問題︰
許多公式不解其推導...
DFT部分也蠻模糊的...
figure 7.28 Low - pass filtering 和 High - pass filtering 指的是什麼?
2007年12月19日 星期三
Week13 - CHAPTER 7
第七章主要是講傅立葉轉換，前面的數學式子有點複雜，所以就大概看過而已，非常的模糊...7.6後的內容就比較跟影像處理有關了，故花了比較多的時間在這，也發現了一些問題。
1.[p.148] 本頁最後一行的the index of the sum是什麼意思呢?
2.[p.169]7.8所說的cutoffs是什麼?課本好像沒解釋。
3.[p.177]7.8.3說利用fspecial會讓高斯的函數等於1，為什麼呢?
1.[p.148] 本頁最後一行的the index of the sum是什麼意思呢?
2.[p.169]7.8所說的cutoffs是什麼?課本好像沒解釋。
3.[p.177]7.8.3說利用fspecial會讓高斯的函數等於1，為什麼呢?
Week14
閱讀心得;
本章再說不管是一個function或是一個陣列或vector的值都可以用不同的function相加去球出最接近但是沒辦法完全相等.DFT也是利用此方法將值轉換成最接近的值.再閱讀時因為數學公式有點複雜所以大概看過去,只知道它就是各種function用來將vector中的element轉成DFT,因為進度還沒完成所以還不大了解DFT跟旋轉和共軛有甚麼關聯.
問題:
p 149 (7.2)Equation 和 p(7.3)Equation 她們兩個的差別有三個(1/N,+,u=>x);她們都DFT,兩個 所轉成的結果是否都相同?
p 150 在[SHIFTING]中有提到將偶數的元素乘以(-1),後面提到X'ofx'=X of x ,是說值與值的距離不變還是???,有點不了解.
p152 ...y0 y1 y2 y3 y0 y1 y2 y3...
...y0 y-3 y-2 y-1 y0 y1 y2 y3...
未甚麼左半邊是y1=>y-3 而右邊是 y1=>y1?
p 152 中提到一組公式 p(u)q(u)(1+exp(4)u)中,是否(1+exp(4)u)係數是決定旋轉的值.
本章再說不管是一個function或是一個陣列或vector的值都可以用不同的function相加去球出最接近但是沒辦法完全相等.DFT也是利用此方法將值轉換成最接近的值.再閱讀時因為數學公式有點複雜所以大概看過去,只知道它就是各種function用來將vector中的element轉成DFT,因為進度還沒完成所以還不大了解DFT跟旋轉和共軛有甚麼關聯.
問題:
p 149 (7.2)Equation 和 p(7.3)Equation 她們兩個的差別有三個(1/N,+,u=>x);她們都DFT,兩個 所轉成的結果是否都相同?
p 150 在[SHIFTING]中有提到將偶數的元素乘以(-1),後面提到X'ofx'=X of x ,是說值與值的距離不變還是???,有點不了解.
p152 ...y0 y1 y2 y3 y0 y1 y2 y3...
...y0 y-3 y-2 y-1 y0 y1 y2 y3...
未甚麼左半邊是y1=>y-3 而右邊是 y1=>y1?
p 152 中提到一組公式 p(u)q(u)(1+exp(4)u)中,是否(1+exp(4)u)係數是決定旋轉的值.
Week14
閱讀心得;
本章再說不管是一個function或是一個陣列或vector的值都可以用不同的function相加去球出最接近但是沒辦法完全相等.DFT也是利用此方法將值轉換成最接近的值.再閱讀時因為數學公式有點複雜所以大概看過去,只知道它就是各種function用來將vector中的element轉成DFT,因為進度還沒完成所以還不大了解DFT跟旋轉和共軛有甚麼關聯.
問題:
p 149 (7.2)Equation 和 p(7.3)Equation 她們兩個的差別有三個(1/N,+,u=>x);她們都DFT,兩個 所轉成的結果是否都相同?
p 150 在[SHIFTING]中有提到將偶數的元素乘以(-1),後面提到X'ofx'=X of x ,是說值與值的距離不變還是???,有點不了解.
p152 ...y0 y1 y2 y3 y0 y1 y2 y3...
...y0 y-3 y-2 y-1 y0 y1 y2 y3...
未甚麼左半邊是y1=>y-3 而右邊是 y1=>y1?
p 152 中提到一組公式 p(u)q(u)(1+exp(4)u)中,是否(1+exp(4)u)係數是決定旋轉的值.
本章再說不管是一個function或是一個陣列或vector的值都可以用不同的function相加去球出最接近但是沒辦法完全相等.DFT也是利用此方法將值轉換成最接近的值.再閱讀時因為數學公式有點複雜所以大概看過去,只知道它就是各種function用來將vector中的element轉成DFT,因為進度還沒完成所以還不大了解DFT跟旋轉和共軛有甚麼關聯.
問題:
p 149 (7.2)Equation 和 p(7.3)Equation 她們兩個的差別有三個(1/N,+,u=>x);她們都DFT,兩個 所轉成的結果是否都相同?
p 150 在[SHIFTING]中有提到將偶數的元素乘以(-1),後面提到X'ofx'=X of x ,是說值與值的距離不變還是???,有點不了解.
p152 ...y0 y1 y2 y3 y0 y1 y2 y3...
...y0 y-3 y-2 y-1 y0 y1 y2 y3...
未甚麼左半邊是y1=>y-3 而右邊是 y1=>y1?
p 152 中提到一組公式 p(u)q(u)(1+exp(4)u)中,是否(1+exp(4)u)係數是決定旋轉的值.
Week14 - CHAPTER 7
第七章關於數學式方面大多看不太懂,雖然部分知道是什麼功用但是仍不知怎麼來的。
p167中的fft2shift(fft2(z));會找不到他的函式是因為版本問題嗎?還是課本的錯誤?
那他的內容和fftshift有什麼不同呢?
p161 DC對影像來說有什麼功用?為什麼figure7.7中平移後會變成點在中間?在這過程間他做了
什麼?
p164 為什麼要看spectrum需要用另外的方法檢視?不能直接使用imshow嗎?(我有用imshow測試過但是
圖出來時，他原本中間的會擴散到旁邊)
p167中的fft2shift(fft2(z));會找不到他的函式是因為版本問題嗎?還是課本的錯誤?
那他的內容和fftshift有什麼不同呢?
p161 DC對影像來說有什麼功用?為什麼figure7.7中平移後會變成點在中間?在這過程間他做了
什麼?
p164 為什麼要看spectrum需要用另外的方法檢視?不能直接使用imshow嗎?(我有用imshow測試過但是
圖出來時，他原本中間的會擴散到旁邊)
Week 14 - Chapter 7 THE FOURIER TRANSFORM
◈ 主題 :
INTRODUCTION TO DIGITAL IMAGEPROCESSING
Chapter 7: THE FOURIER TRANSFORM
◈ 詳細閱讀 (持續更新中...)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 實作心得 :
(工事中...)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 問題 :
① Page 143 第二句話／Introduction
意義不明。
[已解決]
② Page 152 z3下面的第一、二句話／convolution
已知它是怎麼解釋negative indices，但不知道negative indices是
什麼，所以不知道為什麼它要這麼解釋，所以也不知道為什麼會相
等。以上的不知道更有可能是因為我不知道convolution是個什麼樣
的事情。
③ Page 153 程式碼／convolution、circular convolution
看了page152下半頁的例子，再看page153的程式結果，不知道做完
convolution處理後所取的係數為什麼是那七個，不知道做完
circular convolution處理後所取的係數為什麼是那四個。
④ Page 155 倒數五、六行(參Page 146的7.2式)／比較直接做DFT與FFT
的效率
可能不太了解公式，所以不清楚這裡的2^2n與n2^n是如何計算出?
◎ 所有算式
意義不明。(可能需要自己研讀一下微積分與工程數學||b)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 備註 :
由於個人因素導致目前進度嚴重落後，已著手開始反省與逐步完成自己該
做的事。所以這個時間點先發表閱讀至page 155的問題並持續閱讀，本
篇也將持續更新。
INTRODUCTION TO DIGITAL IMAGEPROCESSING
Chapter 7: THE FOURIER TRANSFORM
◈ 詳細閱讀 (持續更新中...)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 實作心得 :
(工事中...)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 問題 :
① Page 143 第二句話／Introduction
意義不明。
[已解決]
② Page 152 z3下面的第一、二句話／convolution
已知它是怎麼解釋negative indices，但不知道negative indices是
什麼，所以不知道為什麼它要這麼解釋，所以也不知道為什麼會相
等。以上的不知道更有可能是因為我不知道convolution是個什麼樣
的事情。
③ Page 153 程式碼／convolution、circular convolution
看了page152下半頁的例子，再看page153的程式結果，不知道做完
convolution處理後所取的係數為什麼是那七個
④ Page 155 倒數五、六行(參Page 146的7.2式)／比較直接做DFT與FFT
的效率
可能不太了解公式，所以不清楚這裡的2^2n與n2^n是如何計算出?
◎ 所有算式
意義不明。(可能需要自己研讀一下微積分與工程數學||b)
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
◈ 備註 :
由於個人因素導致目前進度嚴重落後，已著手開始反省與逐步完成自己該
做的事。所以這個時間點先發表閱讀至page 155的問題並持續閱讀，本
篇也將持續更新。
WEEK14 CH7 The Fourier Transform
在上週上課的時候，老師要我們寫出兩張圖片相融的！
於是乎...我就寫了下面這樣子的...
感覺上就是用固定位置的方式在寫，充分的利用Array位置將值相加、相乘...
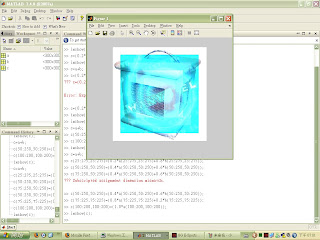
恩...感覺可以用更簡短的Matlab函數來寫...不過想不出來要用什麼
關於重讀CH7之後發現到了一些問題！
問題:[中P.170]
在function cconv中，部分省略...已經確定a陣列與b陣列長度相同
la=length(a);
temp=conv([a a],b);
out=temp(la+1:2*la);
看不懂他怎麼運算的，使用cconv之後會產生小數點後4位?
與課本截然不相同...看不懂了！
應該是還有一些問題...不過一時說不出來那種感覺是什麼，
像是7.8中提到的截頻點對於他的定義上是什麼意思，就感
到有點困惑，它的截頻點應該是先經過DFT的處理之後所
產生出來的，然後我們再對影像做下一步的處理，但是為
什麼經過截頻點處理之後的影像會形成那樣，就搞不懂它
的形成方式....高通與低通濾波器的成像也不同，應該是因
為它們所針對的高頻率與低頻率來處理，所顯現的圖像也
才會有所不同，但有些感覺...就一時也說不上...
於是乎...我就寫了下面這樣子的...
感覺上就是用固定位置的方式在寫，充分的利用Array位置將值相加、相乘...
恩...感覺可以用更簡短的Matlab函數來寫...不過想不出來要用什麼
關於重讀CH7之後發現到了一些問題！
問題:[中P.170]
在function cconv中，部分省略...已經確定a陣列與b陣列長度相同
la=length(a);
temp=conv([a a],b);
out=temp(la+1:2*la);
看不懂他怎麼運算的，使用cconv之後會產生小數點後4位?
與課本截然不相同...看不懂了！
應該是還有一些問題...不過一時說不出來那種感覺是什麼，
像是7.8中提到的截頻點對於他的定義上是什麼意思，就感
到有點困惑，它的截頻點應該是先經過DFT的處理之後所
產生出來的，然後我們再對影像做下一步的處理，但是為
什麼經過截頻點處理之後的影像會形成那樣，就搞不懂它
的形成方式....高通與低通濾波器的成像也不同，應該是因
為它們所針對的高頻率與低頻率來處理，所顯現的圖像也
才會有所不同，但有些感覺...就一時也說不上...
2007年12月13日 星期四
Week 14 CH7
對傅立葉了解的不多 ,查了一些資料
得到傅立葉轉換能把任意的時域函數以數學方法轉換成頻域函數
不過沒學過真的不知道數學試試怎麼出來的.
p152 p(u)=1+2u+3u^2+4u^3
為什麼要這樣做?
conv也不太清楚,只知道2個矩陣長度相加減1
得到傅立葉轉換能把任意的時域函數以數學方法轉換成頻域函數
不過沒學過真的不知道數學試試怎麼出來的.
p152 p(u)=1+2u+3u^2+4u^3
為什麼要這樣做?
conv也不太清楚,只知道2個矩陣長度相加減1
WEEK14 CH7
1維的DFT
1維DFT的特性 (線性 平移 共軛對稱 旋積 快速D傅利葉轉換(FFT))
2維DFT
2維DFT的特性(DFT 當成空間濾波器使用 分離性 線性 旋積定理 DC指數 平移 共軛對稱
掩飾DFT轉換的結果)
DC係數是指DFT的F(0,0) =>還是不懂
濾波器:將遮照下所有單員分別乘上一個固定的數值然後加起來
邊緣的問題可以假設所有方向拼貼填滿，
那遮罩就不會有無影像直可以運算的狀況發生
這章真的很複雜都是數學很多都是有看沒有懂，對於DFT還是不怎麼了解
P152 153 convolution 看不懂= =
1維DFT的特性 (線性 平移 共軛對稱 旋積 快速D傅利葉轉換(FFT))
2維DFT
2維DFT的特性(DFT 當成空間濾波器使用 分離性 線性 旋積定理 DC指數 平移 共軛對稱
掩飾DFT轉換的結果)
DC係數是指DFT的F(0,0) =>還是不懂
濾波器:將遮照下所有單員分別乘上一個固定的數值然後加起來
邊緣的問題可以假設所有方向拼貼填滿，
那遮罩就不會有無影像直可以運算的狀況發生
這章真的很複雜都是數學很多都是有看沒有懂，對於DFT還是不怎麼了解
P152 153 convolution 看不懂= =
WEEK13 CH7 The Fourier Transform
剛看7.1的介紹就覺得這章很有難度
看到7.2時還能理解傅立葉轉換可以用來分析訊號內究竟有什麼樣的訊息
一個有週期性的函數可以被寫成sin或cos的和
如 7.1 f(x)=sinx+1/3sin3x+1/5sin5x+1/7sin7x...
看到p.145開始有見鬼的感覺....熟悉度近似於0
再看下去肯定睡著所以到google搜尋fourier transform
找到一篇李家同教授的paper其中有講到7.3的離散傅立葉轉換比較有感覺一點(是中文的)
參考了Matlab7程式設計的書
Matlab 有提共兩個函數可求得傅立葉轉換和他的逆運算
fourier(f,t,w)
ifourier(F,w,t)
稍微試了一下兩個函數不太能夠掌握，尤其不太了解參數的用法
看到7.2時還能理解傅立葉轉換可以用來分析訊號內究竟有什麼樣的訊息
一個有週期性的函數可以被寫成sin或cos的和
如 7.1 f(x)=sinx+1/3sin3x+1/5sin5x+1/7sin7x...
看到p.145開始有見鬼的感覺....熟悉度近似於0
再看下去肯定睡著所以到google搜尋fourier transform
找到一篇李家同教授的paper其中有講到7.3的離散傅立葉轉換比較有感覺一點(是中文的)
參考了Matlab7程式設計的書
Matlab 有提共兩個函數可求得傅立葉轉換和他的逆運算
fourier(f,t,w)
ifourier(F,w,t)
稍微試了一下兩個函數不太能夠掌握，尤其不太了解參數的用法
台北藝術節
這次去西門町的紅樓看數位藝術節，讓我覺得收穫很多。
很仔細的逛完了所有的作品，印象比較深刻的也不少；
一進去聽的"聲音藝術"，我對於"OCEANIC"最有興趣，
也讓我聽了很久，陣陣的海浪聲，彷彿到了海邊，
很難想像這樣自然的聲音，是用軟體加工變化而成的。
"電動椅"這個展覽也讓我覺得很神奇，看一張椅子從破碎
到自己組合完成，要考慮的因素有很多：要怎麼感應椅子
的每個部位，要怎麼計算角度讓椅子站起來等等，真的很
佩服這些作品的主人。
"哈迪斯可"也是讓我覺得很感興趣的展覽之一，利用16個硬
碟配合簡單的開關指令，而敲擊出一些簡單的節奏，
我覺得作者真的很有創意。
整個展覽當中，"互動音樂桌"算是我最喜歡的作品，
看這些小方塊如何彼此連結產生音樂，左右旋轉還可
以控制速度，這個展覽也是讓我停留最久的一個吧。
以控制速度，這個展覽也是讓我停留最久的一個吧。
其他還有一些很有趣的作品，就不多作介紹了。
台北藝術節
首先，要先說個抱歉=..=因為上禮拜搞婚禮然後瘋狂帶合唱......所以沒自己的時間做作業....不過也很高興合唱得獎囉!!!
所以把上次該交的補上來，希望老師別揍我~~XD
台北藝術節阿，真他O的不是人在去的地方....每次紅樓都人那麼多，下次要在非假日去，不過人太多了，根本就是在跨年現場的情況，所以挑最空曠的地方拍照了，沒地方站了，雖然一路上走馬看花，不過看了很多超妙的東西，印象蠻深刻的是一進去的那個大地圖，把台灣各地的人都串連起來還不賴，還有水波的音樂，很開心可以看到台灣的多媒體發展，但我還是比較希望看到新的玩意兒，因為這些在去年跟前年，美國日本跟瑞典的展覽，都做過類似的作品，感覺幾乎都換湯不換藥，只是中文化了些東西就呈現上來了，但是，能在眼前碰到這些東西依然很開心，我想介紹大家也都去看了也貼出來了，所以我就不在作介紹而是說說去的感想。我是個很喜歡設計的學生，所以自然而然的會去看一些設計的書籍，當我看到作品第一個想到的就是原創者的概念，並不是說台灣的作品不好，而是，本次的藝術節有點像畢業聯展，讓我覺得新一代設計展的創意跟藝術比較能表現出藝術的價值，或許不太能做比較。但我還是蠻期待之後藝術節能再看到更創新的東西。
台北數位藝術節
只是不好操作
這次展覽的東西非常多，雖然只有一些有興趣
就舉一些有興趣的東西講好了...
1.特殊面板上可以透過光來讓影子顯現在面板上，就像這樣
2.不知道它是怎麼弄的，透過碰觸螢幕來讓裡面的人物移動
感覺好像動畫...蠻神奇的
3.全球地圖....還蠻有趣的，操作比較難，不過可以找到某個指定地點內
的東西，像我們找到桃園銘傳
這些大概是比較有興趣的東西，數位展真的蠻有趣的
有許多創新的想法，期待下一次的數位展
這次展覽的東西非常多，雖然只有一些有興趣
就舉一些有興趣的東西講好了...
1.特殊面板上可以透過光來讓影子顯現在面板上，就像這樣
2.不知道它是怎麼弄的，透過碰觸螢幕來讓裡面的人物移動
感覺好像動畫...蠻神奇的
3.全球地圖....還蠻有趣的，操作比較難，不過可以找到某個指定地點內
的東西，像我們找到桃園銘傳
這些大概是比較有興趣的東西，數位展真的蠻有趣的
有許多創新的想法，期待下一次的數位展
台北數位藝術節-玩開 心得
這次的台北數位藝術節讓我看到了體驗很多種創作的東西從一開使進門就讓我有點覺得很新奇的一些作品就是聲音藝術這些聲音的藝術覺得聽起來很清澈的感覺，以風和海等等的聲音，再來也讓我覺得特別的是聲音就是走道中間的數位音像。而到後面的重頭戲就是有一些的很厲害的遊戲。
例:1.互動音樂桌
2.電動椅，會自己突然的像炸開的方式椅子的分裂了，又突然的結合在一起。
3.雙打
4.哈迪斯可 
5.戲水戲，只要去動一動桌上的水就會有聲音出現。
6.玩劇的遊戲就是拿著一個木頭的東西動一動就可以控制螢幕上的兵馬俑的人讓他們跳舞。
7.光之滾刷，最讓我覺得很好玩，他運用光就可以在牆壁上寫出你要的字，而工作人員還幫我拍張照在牆壁上用滾刷就可以畫出來的你臉，也是最多人最熱鬧大家都在玩的地方。
8.雷射塗鴉，也很厲害大家拿著一隻綠色光點的筆就可以在的牆壁上隨心所以的畫出來，也是最樂門的一個遊戲。
2007年12月5日 星期三
week11 ch6
1.計算線性內插法? bicubic內插法和bilinear內插法都是其中的一種? 指的是他有很多其它的?
2.使用bicubic內插法，會覺得bicubic的圖比bilinear的圖更圓滑一點.但是期期我看不懂p.133裡面的運算在做什們..
2.使用bicubic內插法，會覺得bicubic的圖比bilinear的圖更圓滑一點.但是期期我看不懂p.133裡面的運算在做什們..
week11 期中報告
學習心得:這堂課是由MATLAB當作工具來進行對影像的處理，因為MATLAB本身參數多我背不太起來，其實我都是想到要做什們，在去課本翻指令實行，慢慢的有些指令也慢慢記起來了，對於現在的我來說得到的是會使用MATLAB下達指令來更改圖片的值，"有些事其實真的是去做了以後才知道結果"，在MATLAB上面確實也是如此，有很多的事物也和當初我想的不太一樣，對於圖片的RGB分別的概念也更加清楚了一點，大概就是這樣吧.